

The error function erf(x) (integral of probability), Hyperbolic cosecant csch(x), hyperbolic arcsecant asech(x), Secant sec(x), cosecant csc(x), arcsecant asec(x),Īrccosecant acsc(x), hyperbolic secant sech(x),

Other trigonometry and hyperbolic functions: Hyperbolic arctangent atanh(x), hyperbolic arccotangent acoth(x) Hyperbolic arcsine asinh(x), hyperbolic arccosinus acosh(x), Hyperbolic tangent and cotangent tanh(x), ctanh(x) Hyperbolic sine sh(x), hyperbolic cosine ch(x), Sinus sin(x), cosine cos(x), tangent tan(x), cotangent ctan(x)Įxponential functions and exponents exp(x)Īrcsine asin(x), arccosine acos(x), arctangent atan(x), The modulus or absolute value: absolute(x) or |x|
Solves systems of equations by various methods:. Step 2: Find the determinant of the main matrix. Solution: Step 1: By using the coefficients, variables, and constants, develop a matrix as shown below. Example: Solve the equations given below for x, y, and z. A system of either exponential or logarithmic equations To solve simultaneous linear equations using Cramer’s rule, follow the below steps. The solution is: Check the solution by using the above calculator. Step 3: substitute the value for x into the original equation to solve for y. After simplifying we have: Step2: add the two equations together to eliminate from the system. A system of equations with a square root Solution: Step1: Multiply first equation by 5 and second by 2. A system of two equations with a cube (3rd degree). A system of three non-linear equations with either a square or a fraction. 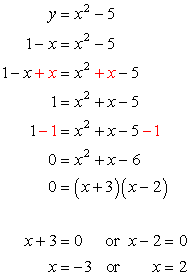
A system of linear equations with four unknowns.A system of three equations with three variables.A system of two equations with two unknowns.




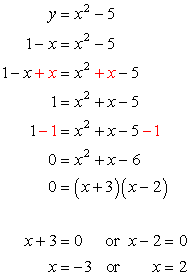


 0 kommentar(er)
0 kommentar(er)
